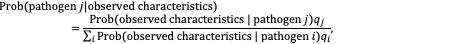In 2018, the World Health Organization added “Disease X” to its list of priority diseases, alongside diseases like Ebola virus disease and SARS. Disease X is representative of infectious agents that are not currently known to cause cases in humans. In other words, it denotes the possibility of an epidemic of a disease that we have never seen before.
Could a devastating epidemic of Disease X in fact be occurring now? The Chinese city of Wuhan, with a population of 11 million people, is experiencing an outbreak of cases of pneumonia. This outbreak is due to a virus that appears to have transitioned from animals into humans at Huanan seafood wholesale market in Wuhan, and new infections are now being generated by sustained human-to-human transmission. As of 23 January, this outbreak has caused over 500 confirmed cases in total, including 17 deaths. The virus has spread elsewhere in China and to other countries, specifically South Korea, Thailand, Japan and USA. As a precautionary measure, the transport systems in Wuhan and the nearby city of Huanggang have been shut down, and travel in and out of the cities has been advised against.
Mathematical modelling is an invaluable tool for forecasting and planning interventions during outbreaks, particularly when the pathogen driving the outbreak is well understood. However, in the first few days of an outbreak, the infectious agent may not be known, since virological tests take time to identify the specific pathogen causing disease unambiguously. This raises the question: can the infectious agent be inferred early in an emerging outbreak, before the results of virological tests become available?
Oxford Mathematician Robin Thompson and colleagues from the laboratory of Prof. Hiroshi Nishiura from Hokkaido University, Japan have been conducting real-time analyses to compare characteristics of the current outbreak with those of previous outbreaks driven by pathogens of known aetiology. As more information is becoming available, this analysis is being updated to reflect new knowledge about the ongoing outbreak. By applying Bayes’ rule, the relative probability that the current outbreak is driven by each of a list of known candidate pathogens can be obtained:
in which the variables represent the a priori probability that the ongoing outbreak is driven by candidate pathogen i.
This provides relative probabilities that each of the candidate pathogens is the causative agent of the ongoing outbreak. This analysis can be extended to investigate whether or not the characteristics of the current outbreak are similar to those of outbreaks of any of the known candidate pathogens. If the ongoing outbreak appears different to any seen previously, then it is most likely that the outbreak is due to Disease X – a disease that we have never seen before.
Genome sequencing has revealed that the virus driving the current outbreak has some similarities to the SARS coronavirus, which caused a major epidemic in 2002-03. Fortunately, it appears that the case fatality rate in the current outbreak is lower than for SARS, i.e. a lower proportion of infected individuals are dying. However, for SARS, epidemiological factors (e.g. the small proportion of onward infections occurring prior to symptoms) allowed the outbreak to eventually be brought under control. Exactly how similar the current outbreak is to that SARS outbreak will become increasingly clear over the next few days and weeks. Maths will provide a key tool for understanding transmission of the virus, as well as potential interventions.
Update from Robin Thompson (25/1/2020): We have been conducting a study to predict the risk of sustained transmission of the China coronavirus in UK. Given the recent news of cases in France, it is a matter of time before there is a confirmed case in the UK. What is less clear, however, is the risk that an imported case will generate a chain of sustained transmission. We have estimated this risk to be 0-37%, depending on the time between the imported case showing symptoms and being isolated. Rigorous surveillance is therefore of paramount importance.
Story courtesy of the Mathematical Institute